Ho già accennato in diversi post a quanto lo standard di cifratura DES sia vulnerabile. Adesso cerchiamo di capire il perchè, andando ad analizzare la logica che ne regola il funzionamento.
Innanzitutto la sigla DES sta per Data Encryption Standard, ed è un sistema di cifratura adottato come standard dal governo degli Stati Uniti d’America nel 1976. L’algoritmo su cui si basa è il DEA (Data Encryption Algorithm), evoluzione di un altro algoritmo di cifratura, il Lucifer, sviluppato presso i laboratori della IBM da Horst Feistel (ideatore della rete omonima). Il DEA, sostanzialmente, è proprio una rete di Feistel ed il suo funzionamento può essere studiato utilizzando il solito approccio, ovvero partendo dai blocchi più esterni fino ad arrivare a quelli più interni.
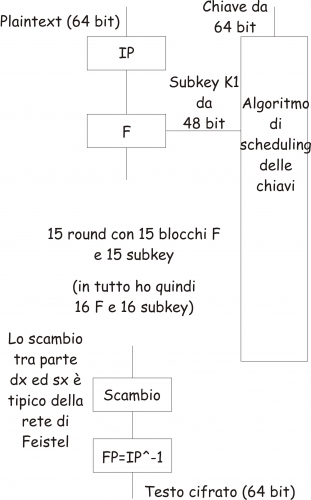
Passiamo quindi alla descrizione dell’algoritmo in questione. Un esempio della sua struttura esterna è presente nella figura seguente:
Il DEA si avvale di un cifrario a blocchi, il quale riceve in ingresso una stringa di testo di lunghezza fissa (plaintext – testo in chiaro) e la trasforma, mediante una serie di operazioni complesse, in un’altra stringa della stessa lunghezza, però cifrata. Nel caso del DES la dimensione di ogni blocco del cifrario è pari a 64 bit. Nel caso in cui il testo in chiaro da cifrare dovesse essere superiore ai 64 bit, esso verrà suddiviso in blocchi da 64 bit ciascuno (aggiungendo eventualmente del padding). Ogni blocco verrà quindi dato in pasto ad un cifrario e gli output così generati verranno combinati tra di loro.
E’ bene notare che IP (Initial Permutation) ed FP (Final Permutation, altrimenti conosciuta come IP^-1) non hanno alcun ruolo nell’ambito della cifratura vera e propria, ma sono state aggiunte per facilitare il caricamento dei vari blocchi di bit sui dispositivi hardware tipici degli anni ’70.
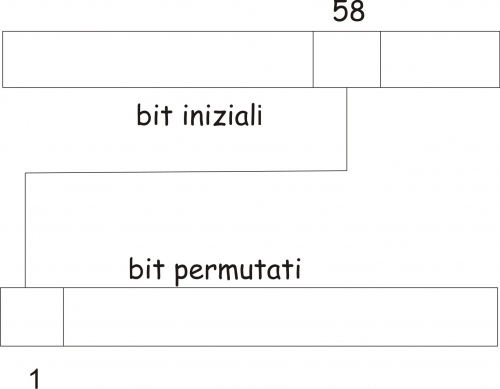
Vediamo ora cosa succede all’interno dell’IP
Ciò significa che il 58-esimo bit della sequenza di input (derivante dal testo in chiaro) verrà spostato in prima posizione della sequenza di output, il 50-esimo bit della sequenza di input verrà spostato in seconda posizione della sequenza di output e così via (seguendo sempre delle regole prefissate). Alla fine dell’IP avremo la seguente situazione (rappresentata in forma matriciale per semplicità, anche se in realtà è un vettore):
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
che, come si può notare, è una matrice 8×8 (contiene 64 elementi, ovvero i 64 bit di input permutati).
Ora che abbiamo visto cosa succede all’interno del blocco identificato dalla sigla IP, è facile andare a descrivere cosa succede in FP. Tale blocco viene anche identificato come IP^-1 poichè non fa altro che invertire le operazioni svolte da IP. Ecco allora che la matrice 8×8 relativa all’output prodotto dal blocco in questione è la seguente:
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
Osserviamo tale matrice. Il bit pari a 1, nella matrice risultate associata all’IP, si trovava in posizione 40. Al termine della FP il bit 40 si troverà in posizione 1. Discorso analogo vale per il bit 2, che nella matrice relativa all’IP si trovava in posizione 8, quindi nella matrice prodotta dalla FP l’8 si troverà in posizione 2 (e così via).
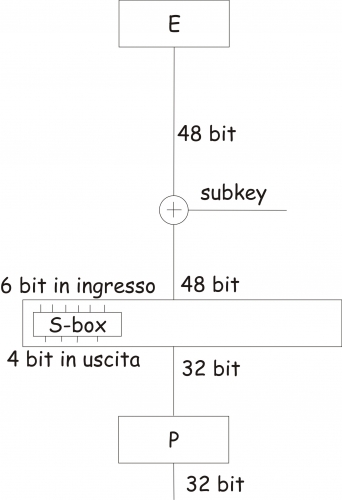
Vediamo adesso cosa succede all’interno del blocco F (ovvero la funzione di Feistel). Essa, sostanzialmente, opera su mezzo blocco per volta (formato da 32 bit) e consiste in 4 passi, illustrati di seguito:
1) Espansione: il mezzo blocco da 32 bit viene espanso a 48 bit utilizzando la cosiddetta permutazione di espansione (contrassegnata proprio con E nello schema), che duplica alcuni bit. Ciò è necessario in quanto successivamente si dovrà effettuare uno XOR con una della 16 subkey da 48 bit prodotte dallo scheduler delle chiavi, e come sappiamo, è impossibile effettuare tale operazione tra sequenze di bit di lunghezza diversa. Ma come avviene effettivamente tale espansione? Semplicemente ripetendo 2 volte i bit contenuti all’interno di 16 posizioni della matrice prodotta dall’IP. Tali posizioni sono “standard” e furono scelte appositamente dall’NSA.
2) Miscelazione con la chiave: viene calcolato lo XOR tra il risultato dell’espansione ed una delle 16 subkey da 48 bit.
3) Sostituzione: I 48 bit che costituiscono il risultato dello XOR tra la subkey ed il semiblocco espanso andranno in ingresso ad 8 S-box. Ciascuna S-box riceve in ingresso 6 bit (6×8 = 48) e restituisce in uscita 4 bit (4×8 = 32). Quindi l’output complessivo delle 8 S-box sarà proprio pari a 32 bit.
Ma come operano effettivamente le S-box? Supponiamo che i 6 bit in ingresso ad una delle 8 S-box siano 110010. La S-box che li riceve in ingresso li trasformerà in modo non lineare, ovvero S-box(a1 XOR s1) != S-box(a1) XOR S-box(s1), dove a1 è il semiblocco ed s1 è la chiave.
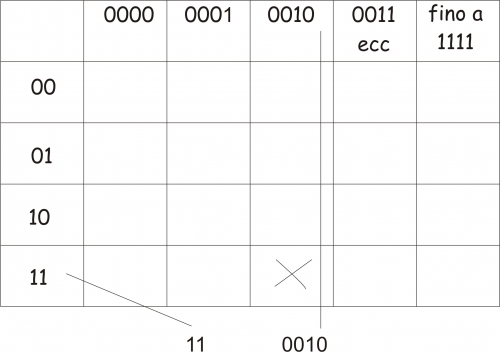
La tabella usata dalle S-box e nella fattispecie da quella che ha ricevuto in ingresso la sequenza 110010, è simile alla seguente:
Dove la posizione della tabella in cui verrà salvata la sequenza è identificata dalla X. Occorre notare, inoltre, che in ogni cella vi sarà un numero compreso tra 1 e 15 (ovvero i valori decimali rappresentabili mediante i 4 bit di output).
I 32 bit così ottenuti, infine, costituiranno l’input di una Permutation Box, identificata con la lettera P, la quale provvederà a ricombinarli per assemblare il seguente output:
| 16 | 7 | 20 | 21 |
| 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 |
| 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 |
| 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 |
| 22 | 11 | 4 | 25 |
Ma qual è l’effettiva utilità del blocco E, delle S-Box e del blocco P? Semplicemente quella di fornire il giusto grado di confusione e diffusione all’algoritmo considerato. Inoltre, sono proprio le S-box a rendere la cifratura non lineare e quindi difficilmente violabile.
Vediamo adesso come avviene lo scheduling delle chiavi. In soldoni, viene ricevuta in ingresso una chiave da 64 bit (56 bit effettivi + 8 bit per il controllo di parità) e restituite in uscita 16 sottochiavi da 48 bit ciascuna. Ma perchè proprio 16 sottochiavi? Perchè 16 è il numero minimo di round per garantire al DEA una buona resistenza contro una tecnica chiamata “crittoanalisi differenziale”, ideata ufficialmente intorno agli anni ’90. Però, il fatto che l’algoritmo DEA utilizzi proprio 16 round e quindi 16 sottochiavi (una per round), può (giustamente) indurci a credere che gli studiosi afferenti all’NSA conoscessero tale tecnica già durante gli anni ’70.
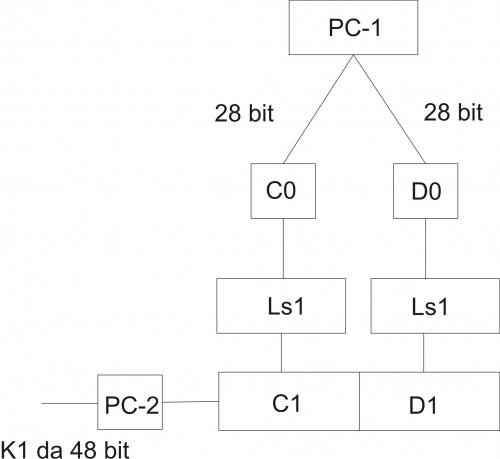
Ecco lo schema che rappresenta lo scheduling delle chiavi:
In ingresso a PC-1 (ovvero Permuted Choise – 1) ho 64 bit (come detto in precedenza). Da questi 64 bit verranno scartati gli 8 bit di parità fino ad ottenere una chiave da 56 bit (essi verranno inoltre permutati). Tale chiave verrà quindi divisa in due parti da 28 bit ciascuna, chiamate rispettivamente C0 e D0. Esse andranno in ingresso ad LS1, che ne effettuerà uno o due shift a sinistra per ricavare C1 e D1. In generale, LS[i] esegue uno o due shift a sinistra su C[i-1] e D[i-1] per ricavare C[i] e D[i]. Ad esempio:
Infine, C1 e D1 vengono passate in ingresso a PC2 (Permutation Choise – 2), che produce il seguente output di permutazione:
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
generando la sottochiave K1 da 48 bit.
Ovviamente tali operazioni si ripetono per tutti e 16 i round.
Ma perchè DES è insicuro? Semplicemente perchè utilizza chiavi troppo piccole (di soli 56 bit), vulnerabili ad attacchi bruteforce, che rendono deltutto inutile la robustezza del DEA contro gli attacchi basati sulla crittoanalisi.
Alcune osservazioni
Per DES vale la seguente regola:
M’ = E(K,M)
M = D(K,M’) e non M = E(K,M’)
dove E equivale all’operazione di cifratura (Encryption), la D a quella di decifratura, K è la chiave, M il messaggio in chiaro ed M’ quello cifrato.
In particolare, l’operazione di cifratura e decifratura sono identiche se e solo se tutte le sottochiavi sono uguali (ciò si verifica soltanto per le 4 chiavi “deboli”). Esistono inoltre le cosiddette chiavi sottodeboli, in cui corrispondono solo alcune delle sottochiavi.
Curiosità
Per molto tempo si è creduto che l’NSA conoscesse un sistema per decifrare facilmente i messaggi criptati tramite DES, in modo da tenere sotto controllo il maggior numero possibile di conversazioni “private”. Per la precisione, si riteneva che tale sistema si basasse su un uso particolare delle S-box, il cui funzionamento è rimasto nascosto a lungo, proprio per volere dell’NSA (security through obscurity). Quando però le S-box vennero pubblicate e descritte dettagliatamente, questa tesi cadde istantaneamente. Essa, nonostante ciò, fu uno dei motivi principali che resero il DEA uno degli algoritmi di cifratura più studiati della storia (soprattutto in ambito universitario).
Un’altra curiosità riguarda invece la chiave da 56 bit: perchè utilizzare una chiave di dimensioni così ridotte? Molti affermano che la vera ragione stia sempre nella volontà dell’NSA di controllare il contenuto dei messaggi cifrati, stavolta mediante bruteforce (la tecnologia che consentiva di perpetrare un attacco di questo tipo durante gli anni ’70 era, in teoria, prerogativa dell’NSA). Ovviamente, per la disponibilità tecnologica dell’epoca, era impensabile effettuare attacchi a forza bruta (entro tempi accettabili) contro chiavi di dimensioni maggiori.
Il post termina qui, a presto.