Usando continuamente lo SHA-1 come algoritmo di cifratura per le password salvate in MySQL, ho deciso di capire meglio come funziona e qual è la logica secondo la quale vengono creati i digest (impronte). Infatti, lo SHA-1 (acronimo di Secure Hash Algorithm), è il tipico esempio di algoritmo di cifratura one-way, ovvero non reversibile. Ciò significa che una volta cifrato il messaggio, non deve essere possibile dal punto di vista computazionale risalire al testo in chiaro. Nonostante questo, lo SHA-1 presenta comunque delle vulnerabilità: recentemente è stato infatti scoperto un attacco basato sulla crittoanalisi in grado di generare facilmente delle collisioni (sono proprio le collisioni il tallone di Achille di tutti gli algoritmi di cifratura one-way). Nella fattispecie, si ha una collisione quando due testi in chiaro producono lo stesso digest, compromettendo quindi in tutto o in parte la sicurezza delle informazioni criptate.

Fatta questa breve premessa, vediamo più da vicino il meccanismo utilizzato dallo SHA-1 per cifrare i messaggi.

Supponiamo che la stringa che si vuole cifrare abbia dimensione (in bit) inferiore a 2^64. In questo caso sarà necessario effettuare del padding (ovvero del riempimento), in modo da rendere la lunghezza L del messaggio espanso un multiplo intero di 512 bit (Nx512).

Il padding avviene nel seguente modo: si aggiunge in coda alla sequenza di bit che identifica il messaggio cifrato un bit pari a 1, diversi bit pari a 0 e due word da 64 bit ciascuna (128 bit in tutto). Esse servono proprio a rappresentare la lunghezza L del messaggio prima che su di esso venga effettuato del riempimento. Ma andiamo per ordine, supponiamo che il messaggio da cifrare sia identificato dalla seguente stringa di bit:

00010001 11001100 111001101 11110011 11101111

come si può facilmente notare, la lunghezza L della sequenza di bit è pari a 40 (L = 40). Poichè tale lunghezza è inferiore a 2^64 bit, allora devo usare del padding.

1) Aggiungo un bit pari a 1 in coda alla sequenza di bit sopra riportata:

00010001 11001100 111001101 11110011 11101111 1

2) Aggiungo tanti bit pari a 0 quanti ne servono per ottenere una dimensione pari a 448 bit (448 – 41 = 407 zeri), in modo tale da avere, successivamente all’aggiunta delle due word da 128 bit complessivi, una lunghezza del messaggio espanso pari a 512 bit (dimensione usata appositamente per rendere più esplicativo l’esempio).

00010001 11001100 111001101 11110011 11101111 10000000 00000000 00000000 00000000 ecc.

3) Creo le due word da 64 bit ciascuna. Se la dimensione del messaggio (ovvero L) è inferiore a 2^32 bit, la prima word sarà costituita da 64 bit pari a 0. La seconda word, invece, è la conversione in binario del numero intero 40, che è proprio la lunghezza L. Quindi avrò:

00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 prima word;

00000000 00000000 00000000 00000000 00000000 00000000 00000000 00101000 seconda word.

Una volta che il padding verrà completato, il testo espanso ci apparirà nel modo seguente:

00010001 11001100 111001101 11110011 11101111 10000000 00000000 00000000 00000000 ecc… 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00101000

Bene, supponiamo ora che il messaggio espanso abbia una dimensione che sia un multiplo di 512 bit. Esso verrà quindi suddiviso in Mn (leggasi M con n, dove n è il pedice) blocchi da 512 bit ciascuno. Tali blocchi andranno in ingresso ad una funzione F, il cui funzionamento verrà descritto più avanti. Occorre notare che la prima funzione F, quella cioè relativa al blocco M1, riceverà in ingresso 5 word da 32 bit ciascuna (160 bit in tutto) appartenenti ad un IV (vettore di inizializzazione), che chiameremo h0, h1, h2, h3 ed h4.

In particolare, esse vengono inizializzate ai seguenti valori (in esadecimale):

h₀ = 67452301

h₁ = EFCDAB89

h₂ = 98BADCFE

h₃ = 10325476

h₄ = C3D2E1F0

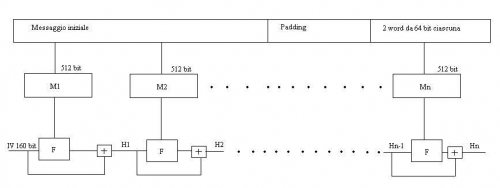
Vediamo come appare lo schema di cifratura dello SHA-1:

Come potete notare, la prima funzione F (da sinistra) riceve in ingresso M1 e l’IV, la seconda riceve in ingresso M2 ed il risultato della somma tra l’IV e l’output della prima funzione F, generando H1 e con questa logica vengono generati H2,H3, H4, fino ad arrivare ad Hn, ovvero il digest vero e proprio (da 160 bit).

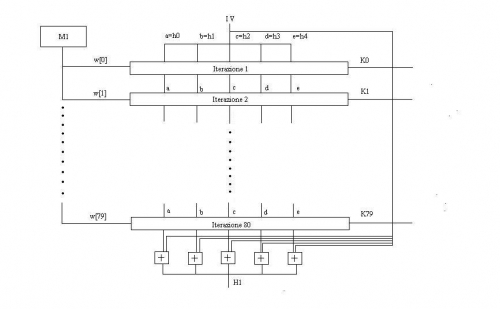
Ma cosa fa effettivamente F? Per capirlo osserviamo il seguente schema che si riferisce al primo blocco, ovvero M1:

 

Il blocco M1 viene suddiviso in 16 blocchetti w (da 0 a 15). Poichè però la funzione F consta di 80 iterazioni, i 64 blocchetti rimanenti (80 in tutto) vengono generati nel modo seguente:

w[t] = (w[t-3] XOR w[t-8] XOR w[t-14] XOR w[t-16]) << 1 con 16<=t<=79

dove << 1 rappresenta uno shift verso sinistra del risultato ottenuto (ed è proprio questa l’unica differenza esistente tra lo SHA, altrimenti conosciuto come SHA-0, e lo SHA-1).

Ogni iterazione riceve in ingresso le word a, b, c, d, ed e (ovviamente coincidenti con h0, h1, h2, h3 ed h4 per la prima iterazione), il blocco w[t] ed una costante additiva Kt, con Kt inizializzata nel modo seguente:

Kt = 5A827999  per 0 <= t <= 19

Kt = 6ED9EBA1 per 20 <= t <= 39

Kt = 8F1BBCDC per 40 <= t <= 59

Kt = CA62C1D6 per 60 <= t <= 79

Ad ogni iterazione viene generata una variabile temporanea TEMP, dove TEMP = (a << 5) + f + e + Kt + w[t] e la funzione f, che dipende da t, ovvero dall’iterazione considerata e dalle word b, c, ed e, sarà data da:

(b AND c) OR ((NOT b) AND d) per 0 <= t <= 19

b XOR c XOR d per 20 <= t <= 39

(b AND c) OR (b AND d) OR (c AND d) per 40 <= t <= 59

b XOR c XOR d per 60 <= t <= 79

Una volta creata la variabile TEMP, l’iterazione effettuerà le seguenti operazioni di sostituzione e di shifting:

1) la variabile TEMP viene salvata in a;

2) la word a viene salvata in b;

3) la word b viene salvata in c e successivamente c viene spostata di 30 posizioni verso sinistra;

4) la word c viene salvata in d;

5) la word d viene salvata in e.

Le word così ottenute andranno in ingresso all’iterazione immediatamente successiva.

Inutile dirvi che comprendere a pieno tale algoritmo di cifratura non è banale come non è per niente semplice cercare di spiegarlo in modo chiaro. Spero comunque di esservi stato d’aiuto.

A presto.