Abbiamo già visto come la cifratura convenzionale riesca a garantire un adeguato livello di protezione contro gli attacchi di tipo passivo, volti cioè all’intercettazione (sniffing) dei dati. Vediamo adesso quali sono le tecniche utilizzate per difendersi contro l’eventuale alterazione (tampering) di uno o più messaggi (attacchi di tipo attivo).

Sia ben chiaro che la cifratura convenzionale, oltre a garantire la riservatezza, riesce anche a soddisfare i requisiti associati all’autenticazione dei messaggi; supponiamo, a tal proposito, che solo mittente (A) e destinatario (B) condividano la chiave di cifratura KAB. Quando il destinatario B andrà a decifrare il messaggio inviato dal mittente A utilizzando la chiave KAB sarà certo che la sorgente del messaggio è quella legittima e che il messaggio stesso non è stato alterato. L’aggiunta di un eventuale numero di sequenza (nel caso di più messaggi) e di un timestamp, preservano il messaggio da eventuali repliche o ritardi di natura malevola.

L’uso della cifratura convenzionale per l’autenticazione dei messaggi, però, ha i suoi pro ed i suoi contro. Infatti, non conviene utilizzare tale approccio nel momento in cui uno stesso messaggio cifrato debba essere inviato in broadcast (portando tutte le macchine della rete ad effettuare operazioni di decifratura dopo averlo ricevuto), oppure nel caso in cui vengano inviati più messaggi cifrati ad una stessa macchina (magari congestionata), la quale si troverebbe costretta ad effettuare ulteriori operazioni di calcolo volte alla decrittazione del messaggio stesso.

Ecco allora che in questi casi risulta molto più conveniente utilizzare altre tecniche per l’autenticazione dei messaggi, quali il MAC (Message Authentication Code).

Tale tecnica prevede che solo mittente (A) e destinatario (B) condividano la chiave segreta KAB (detta SID). Il mittente A, prima di inviare il messaggio M, calcola il MAC, mediante una funzione che ha come argomenti il contenuto del messaggio M e la chiave segreta KAB: MAC=F(KAB, M). Il MAC così generato verrà accodato al messaggio in chiaro M e verrà inoltrato al destinario B.

Una volta ricevuto tale messaggio, B calcolerà a sua volta il MAC del messaggio utilizzando sempre KAB ed il contenuto del messaggio in chiaro (M). Se i due MAC coincidono, il destinatario ha la certezza che la sorgente è quella legittima e che il messaggio non è stato contraffatto.

Il messaggio, comunque, potrebbe essere ancora oggetto di eventuali attacchi di tipo reply oppure di eventuali ritardi dolosi.

Un’altra tecnica ampiemante utilizzata nell’ambito dell’autenticazione dei messaggi prevede l’uso di funzioni HASH. Tali funzioni devono presentare le seguenti caratteristiche:

1) devono essere applicabili a testi in chiaro di lunghezza variabile;

2) devono generare un digest (impronta) di lunghezza fissa;

3) devono possedere una complessità computazionale non elevata, in modo da semplificare la loro implementazione sia a livello software che a livello hardware;

4) dato h (il digest) è computazionalmente impossibile trovare x tale che H(x)=h. In altri termini dato il digest è computazionalmente impossibile trovare il testo in chiaro (x) a partire dal quale il digest stesso è stato generato. Tale proprietà è detta di uniderezionalità o one-way (senso unico);

5) è computazionalmente impossibile trovare y diverso da x tale che H(x) = H(y). In questo caso parliamo di resistenza debole alle collisioni (si ha una collisione quando due testi in chiaro differenti generano lo stesso digest);

6) è computazionalmente impossibile trovare una coppia (x, y) tale che H(x) = H(y). In questo caso parliamo di resistenza forte alle collisioni. La resistenza forte implica la resistenza debole, ma non vale il viceversa.

Le prime 3 proprietà sono di carattere pratico, la quarta e la quinta garantiscono discreti livelli di sicurezza, mentre la sesta consente alle funzioni HASH di resistere ad attacchi piuttosto sofisticati, tra cui l’attacco birthday, il quale riesce a ridurre la robustezza delle funzioni a m-bit da 2^m a 2^m/2.

HASH e cifratura simmetrica

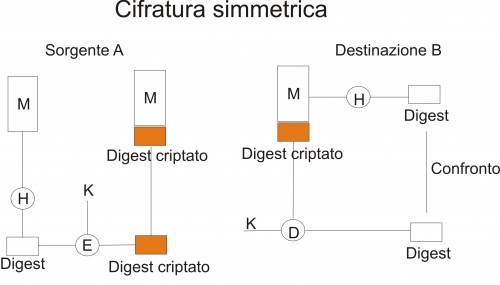
Per aumentare ulteriormente i livelli di sicurezza offerti dalle funzioni HASH si potrebbe utilizzare la cifratura convenzionale (simmetrica). Ad esempio, il mittente A, dopo aver calcolato il digest del messaggio in chiaro M, lo cifra utilizzando un algoritmo (ad esempio DES) ed una chiave K (conosciuta, ovviamente, anche dal destinatario). Una volta ricevuto il messaggio, il destinatario B userà M (il messaggio in chiaro) per calcolare il digest H(M). Successivamente B decifrerà mediante K il digest calcolato dal mittente A ed accodato ad M ed infine effettuerà un confronto tra il digest calcolato direttamente da lui e quello calcolato ed inviatogli dal mittente.

Dal punto di vista computazionale, le funzioni HASH hanno costo lineare (sono sostanzialmente delle somme modulari) ed il DES è molto semplice da implementare a livello hardware, attribuendo a tale approccio un elevata ottimizzazione dal punto di vista delle prestazioni. C’è da dire, però, che il DES è un cifrario a blocchi ed in quanto tale garantisce l’integrità di ogni singolo blocco e non dell’intera sequenza. A titolo di esempio, se il mittente inviasse la sequenza 1|2|3|4 il desinatario potrebbe ricevere 2|1|3|4, alterando il significato del messaggio nella sua interezza. Per ovviare a ciò si dovrebbero utilizzare delle tecniche di concatenazione, le quali, però, sono molto costose.

Infine, in questo caso la resistenza debole alle collisioni deve essere rispettata, in quanto se si riuscisse a trovare un testo in chiaro M’ che generi lo stesso digest del messaggio lecito M, l’attaccante potrebbe sostituire M con M’ senza che il destinatario se ne accorga, compromettendo l’integrità del messaggio (e della fonte). L’unidirezionalità e la resistenza forte, invece, non sono fonte di preoccupazione.

 

HASH e cifratura asimmetrica

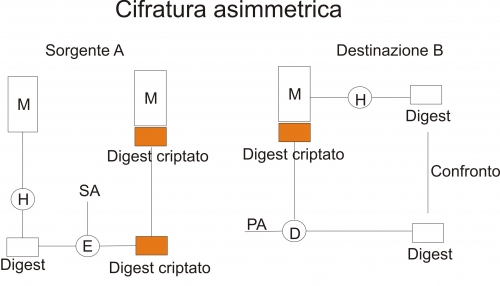
Un altro approccio per irrobustire ulteriormente le funzioni HASH si basa sull’uso della cifratura asimmetrica. Sia, come al solito, A il mittente e B il destinatario. A calcola il digest (H(M)) sul messaggio in chiaro M e successivamente cifra il digest stesso attraverso la sua chiave segreta SA, generando H(M)’. A questo punto accoda il digest cifrato al messaggio in chiaro e lo inoltra al destinatario. Il destinatario, ovvero B, riceve il messaggio in chiaro M concatenato al digest cifrato H(M)’, calcola a sua volta il digest su M e decifra H(M)’ utilizzando la chiave pubblica del mittente, ovvero PA. Se il digest calcolato dal destinatario coincide con quello del mittente allora dovrebbe essere garantita l’autenticità della sorgente e l’integrità del messaggio. Ma è davvero così? La risposta è no. Infatti supponiamo che un attaccante intercetti M||H(M)’ e sostituisca H(M)’ con H(M)”, deliberatamente creato da egli stesso. A questo punto decifra H(M)” utilizzando PA e genera il messaggio in chiaro M”. Il messaggio risulta così alterato e stesso discorso vale per la fonte, anche se il destinatario non si è accorto di quanto avvenuto.

 

HASH e valore segreto

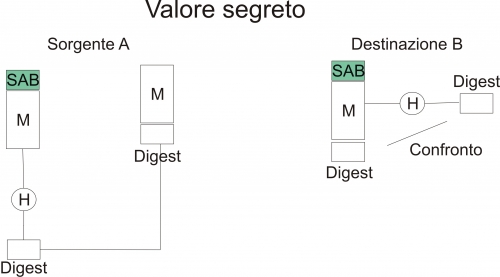
Un altro metodo per rendere ancora più sicure le funzioni HASH riguarda l’uso di un valore segreto, che chiameremo SAB, condiviso da mittente A e destinatario B. Prima di calcolare l’HASH sul messaggio in chiaro M, il mittente concatena SAB ad M e solo dopo ne calcola l’HASH:

C=H(SAB||M). A questo punto A trasmetterà M||C ed appena tale messaggio verrà ricevuto dal destinatario B, quest’ultimo provvederà a concatenare ad M SAB, a calcolare l’HASH ed infine a confrontare il digest così ottenuto con quello inviatogli dal mittente. Se il confronto va a buon fine allora sia messaggio che sorgente possono considerarsi integri.

Una variante di tale approccio viene utilizzato nell’HMAC, che esamineremo in dettaglio nei prossimi post. A presto.