Abbiamo già visto, nei precedenti post, cosa sono i cifrari a blocchi. Adesso cercherò di descrivere le loro possibili modalità di funzionamento.
ECB (Electronic CodeBook)
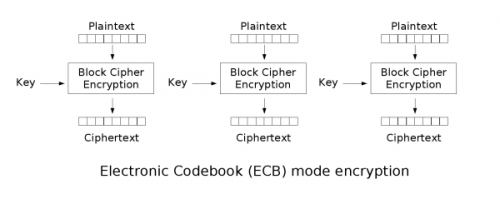
La ECB rappresenta sicuramente la più elementare tra le modalità di funzionamento dei cifrari a blocchi. In particolare, il testo in chiaro, altrimenti conosciuto come plaintext, viene suddiviso in N blocchi di lunghezza fissa, pari a 64 bit, aggiungendo del padding all’ultimo blocco in caso di necessità (ovvero nel caso in cui la lunghezza totale del plaintext non sia un multiplo intero di 64 bit).
E’ bene notare che ogni blocco viene cifrato utilizzando la stessa chiave, quindi, per ogni blocco da 64 bit di testo in chiaro vi sarà il corrispettivo testo cifrato. Ecco perchè parliamo di CodeBook: si può immaginare tale modalità come un grande dizionario in cui è presente una “traduzione” per ogni blocco da 64 bit di testo in chiaro. Questa “traduzione” è appunto il testo cifrato.
Tale modalità di funzionamento dei cifrari a blocchi presenta però una grossa vulnerabilità. Infatti, nel caso in cui occorra cifrare dei testi di grandi dimensioni in cui sono presenti parti ricorrenti, il testo cifrato si ripeterà anch’esso facilitando eventuali attacchi basati sulla crittoanalisi. Ecco allora che risulta necessario utilizzare la ECB per crittografare esclusivamente testi di piccole dimensioni, come le chiavi di cifratura.
CBC (Cipher Block Chaining)
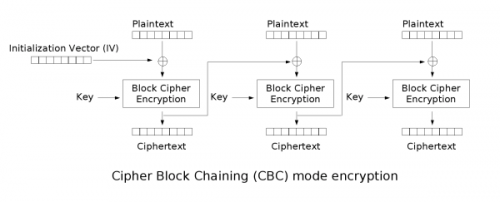
Un’altra modalità di funzionamento dei cifrari a blocchi è la CBC. Essa può essere schematizzata nel modo seguente:
Il testo in chiaro viene suddiviso in blocchi di lunghezza fissa, pari a 64 bit (in modo del tutto analogo alla ECB). Però, prima di dare in pasto il plaintext all’algoritmo di cifratura, esso viene “xorato” con il testo cifrato proveniente dal blocco immediatamente precedente. Per ciò che concerne il primo blocco, non essendoci, ovviamente, blocchi precedenti ad esso, il testo in chiaro viene “xorato” con un vettore di inizializzazione (IV) e successivamente passato in ingresso all’algoritmo di cifratura, il quale utilizzerà sempre la medesima chiave K per ogni blocco. In definitiva, per l’operazione di cifratura avremo:
Cj = E(K, [Cj-1 XOR Pj] ovvero il testo cifrato ricavato dal blocco j-esimo è stato ottenuto cifrando (E) mediante la chiave K il risultato dello XOR tra il testo cifrato del blocco immediantamente precedente (Cj-1) ed il plaintext del blocco considerato (Pj).
La decifratura avviene in modo altrettanto semplice: il testo cifrato viene decifrato utilizzando sempre la stessa chiave K e successivamente il risultato di tale operazione viene “xorato” con il testo cifrato proveniente dal blocco immediatamente precedente. Nel caso del primo blocco, lo XOR viene calcolato considerando il vettore di inizializzazione utilizzato durante la fase di cifratura.
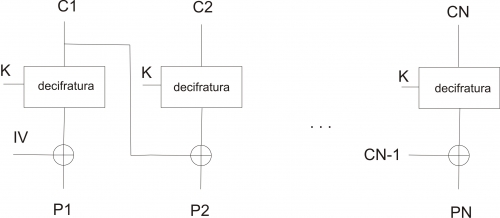
Nella figura sottostante è riportata una schematizzazione dell’operazione di decifratura:
Per dimostrare la validità di tale schema basta fare alcune considerazioni. Si voglia ad esempio decifrare Cj (ovvero il testo cifrato ricavato dal blocco j). Avremo:
Pj = Cj-1 XOR D(K, Cj) = Cj-1 XOR D(K, E(K, [Cj-1 XOR Pj])) = Cj-1 XOR Cj-1 XOR Pj (poichè cifratura e decifratura sono diametralmente opposte ed è come si si “annullassero” a vicenda). Poichè lo XOR di un elemento per se stesso restituisce 0 avremo:
Pj = 0 XOR Pj = Pj (dato che l’elemento neutro dello XOR è proprio lo 0).
Ovviamente, affinchè il testo cifrato possa essere decifrato correttamente, il vettore di inizializzazione deve essere conosciuto sia dal mittente che dal destinatario. Inoltre, l’IV deve essere ben protetto, almeno quanto la chiave. Tale affermazione può essere giustificata dal fatto che un eventuale attacker potrebbe far utilizzare al ricevente un valore diverso associato al vettore di inizializzazione, provocando un’alterazione delle informazioni inviate. A titolo di esempio basta osservare le seguenti formule:
Cj = E(K, [IV XOR P1]
P1 = IV XOR D(K, C1)
P1[i] = IV[i] XOR D(K, C1)[i]
dove l’indice i rappresenta l’i-esimo bit del primo blocco di plaintext (P1), del vettore di inizializzazione (IV) e dell’operazione di decifratura mediante la chiave K del blocco cifrato C1 (D(k, C1)).
Per una proprietà dello XOR si può affermare che:
P1[i]’ = IV[i]’ XOR D(K, C1)[i]
dove l’apice denota il complemento di bit. Questo implica che se l’attaccante modifica i bit del vettore di inizializzazione (calcolandone il complemento, ovvero i bit pari a 1 vengono posti a 0 e viceversa), allora verrà modificato anche il primo blocco di testo in chiaro, cioè P1. In tal caso avremo la modifica dell’intero messaggio, poichè tale alterazione andrebbe ad influire negativamente sulla decifratura dei rimanenti blocchi di plaintext.
CFB (Cipher Feedback)
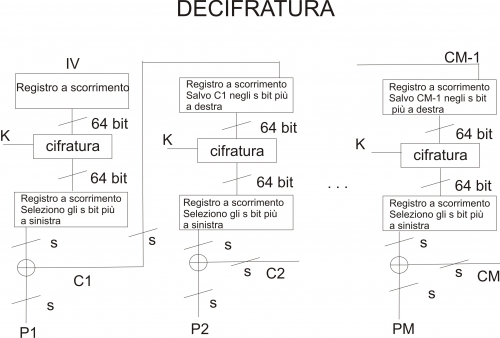
Tale modalità consente di convertire un qualsiasi cifrario a blocchi in un cifrario a flusso. I vantaggi di tale operazione sono molteplici: ad esempio, con i cifrari a flusso non è necessario operare su blocchi di testo aventi lunghezza prefissata, evitando quindi eventuali operazioni di padding e consentendo una cifratura in tempo reale.
Una caratteristica che qualsiasi cifrario a flusso dovrebbe avere riguarda la dimensione del testo cifrato. In particolare, si dovrebbe usare lo stesso numero di bit per rappresentare ciascun carattere del testo in chiaro e del testo cifrato. Nel caso in cui ciò non si verifichi si andrebbe incontro ad uno spreco di potenza in trasmissione.
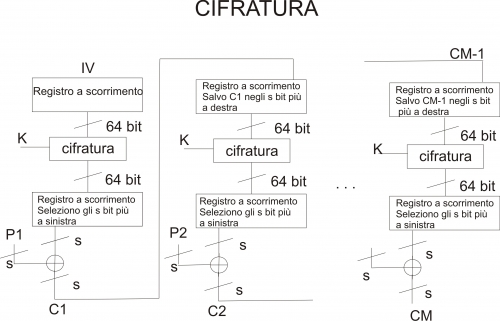
Durante la fase di cifratura, l’ingresso della funzione di crittografia è rappresentata da un registro a scorrimento (shift register) da 64 bit, all’interno del quale, inizialmente, viene memorizzato un vettore di inizializzazione (IV). L’intero contenuto dell’IV (64 bit) viene dato in pasto alla funzione di cifratura. Successivamente, gli s bit più significativi (ovvero quelli più a sinistra) in uscita dalla funzione di crittografia verranno “xorati” con i primi s bit associati al primo blocco di testo in chiaro (P1). In tal modo viene prodotta la prima unità di testo cifrato (C1) che verrà salvata all’interno dello shift-register utilizzato durante la seconda fase di cifratura. Nella fattispecie, gli s bit relativi a C1 rappresenteranno gli s bit più a destra (ovvero quelli meno significativi) dello shift register. Il processo viene reiterato fino all’esaurimento di tutte le unità di testo in chiaro.
Per la decifratura si utilizza lo stesso schema visto in precedenza, solo che in questo caso lo XOR viene calcolato tra gli s bit della funzione di cifratura e le unità di testo cifrato precedentemente calcolate (ovvero C1, C2, ecc.). Il perchè venga utilizzata la funzione di cifratura anche durante la fase di decifratura può essere intuito guardando le seguenti espressioni:
C1 = P1 XOR Ss[E(K, IV)] dove Ss sono gli s bit più significativi (più a sinistra) in uscita dalla funzione di cifratura. Allo stesso modo si ha che:
P1 = C1 XOR Ss[E(K, IV)].
Identico ragionamento va fatto per i passi successivi del procedimento.
Counter (CTR)
Tale modalità è stata introdotta nell’ambito di alcuni protocolli quali ATM (Asynchronous Transfer Mode) ed IPSec (IP Security).
Il suo funzionamento si basa sull’utilizzo di un contatore che (solitamente) ha le stesse dimensioni del blocco di plaintext da cifrare. Questo contatore viene inizializzato ad un certo valore e successivamente viene incrementato di un’unità per ogni blocco successivo. Ciò si rende necessario poichè è essenziale che il valore associato al contatore sia diverso per ciascun blocco da cifrare. Il valore del contatore deve essere diverso anche per ciascun testo che si intende cifrare (mediante una stessa chiave).
Ma perchè questa restrizione? Supponiamo che in ingresso alla funziona di cifratura vi sia un contatore inizializzato sempre allo stesso valore. In questo modo la funzione di crittografia produrrebbe sempre lo stesso output che andrebbe “xorato” con l’i-esimo blocco di testo in chiaro. Nel caso in cui, però, due blocchi di testo in chiaro fossero identici (ad esempio vi è una parola nel testo che si ripete più volte) ciò causerebbe la creazione di due blocchi di testo cifrato identici, facilitando notevolmente la messa in atto di attacchi basati sulla crittoanalisi.
Vediamo ora come viene effettuata l’operazione di incremento su ogni contatore. Supponiamo che ogni blocco di testo in chiaro sia composto da un numero di bit pari a b. L’incremento del contatore può basarsi indifferentemente sull’intero numero di bit che costituisce il blocco di testo in chiaro, ovvero b, oppure su una porzione di esso, che chiameremo m, dove, ovviamente, m<=b. Ogni stringa di m bit può essere facilmente rappresentata mediante un intero x che è strettamente minore di 2^m. A titolo di esempio, supponiamo che b sia pari ad 8 e che m sia pari a 5. Ciò significa che degli 8 bit che costituiscono l’intero blocco di testo in chiaro considero solo gli ultimi 5 bit (che costituiranno il mio contatore), ovvero:
10111110 bit dell’intero blocco;
***11110 bit scelti da me per inizializzare il contatore ed effettuare l’operazione di incremento.
Il massimo valore intero rappresentabile mediante questi cinque bit è pari a 31. Ovviamente 31<32, ovvero di 2^5, ecco perchè ogni stringa di m bit può essere rappresentata mediante un intero x strettamente minore di 2^m.
Incrementiamo adesso la stringa di m bit e vediamo cosa succede:
***11110
effettuo il primo incremento
***11111
effettuo il secondo incremento
***00000
effettuo il terzo incremento
***00001
e così via.
Come schematizzare tale procedura? Semplice, dato x numero intero che rappresenta la stringa di m bit iniziale, la stringa di m bit immediatamente successiva avrà come valore x+1 mod 2^m. Infatti:
***11110 = 30
***11111 = 31
***00000 = 0 (il valore massimo che può assumere la stringa è 31, ergo pongo nuovamente tutto a 0. In altri termini 32 mod 2^5 è uguale a 0).
***00001 = 1
e così via.
Abbiamo già detto che ogni contatore deve essere scelto in modo da non permettere la presenza di contatori uguali all’interno dello stesso messaggio oppure tra messaggi diversi criptati mediante la stessa chiave. A questo punto risulta banale immaginare che tale restrizione si basi principalmente sulla scelta del contatore da utilizzare per il primo blocco del messaggio. In particolare, questo contatore dovrà essere strutturato in modo tale da non assumere valori uguali nel contesto dello stesso messeggio o di tutti i messaggi cifrati con la stessa chiave.
Per soddisfare tale condizione può essere assegnato ad ogni messaggio un nonce, ovvero una stringa univoca (solitamente pari a b/2, se il risultato di tale operazione è un numero dispari bisogna arrotondare) che viene incorporato all’interno di ciascun contatore utilizzato nell’ambito dei blocchi di testo in chiaro. Quindi ogni contatore sarà costituito da N, ovvero il nonce, concatenato con gli m bit che dovranno subire l’incremento:
Tj = N | [j]m, con j che va da 1 a n, dove Tj è il j-esimo contatore, [j]m è la j-esima stringa di m bit da incrementare ed n è il numero di blocchi di plaintext.
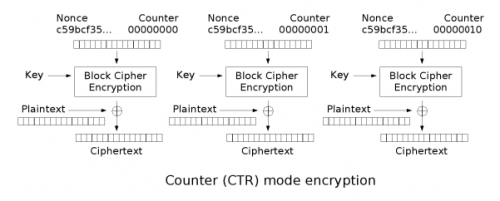
Per completezza ecco una schematizzazione del funzionamento associato al CTR (in fase di cifratura):
I vantaggi che l’uso di tale modalità di funzionamento dei cifrari a blocchi comporta sono molteplici, ovvero:
– semplicità;
– efficienza a livello software;
– efficienza a livello hardware;
– sicurezza dimostrabile.
A presto.